Разделы

• 2.3.1 Уравнение Адамса Вильямсона

2.3 Определение плотности внутри планеты

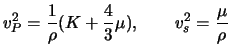
Как мы видели, скорость распространения объемных упругих волн внутри планеты зависит как от упругих постоянных, так и от плотности пород, слагающих Землю. Одной из важнейших задач сейсмологии является определение плотности пород внутри планеты. Обратимся к формулам (2.1), которые перепишем здесь в следующем виде

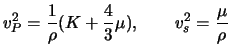
Исключая модуль сдвига, получим . Полученную величину называют сейсмическим параметром и обозначают буквой . Выразим модуль сжатия через сейсмический параметр. Из определения модуля всестороннего сжатия следует . Изменение плотности прямо пропорционально изменению объема, поэтому , следовательно . Отсюда еще одно определение сейсмического параметра: .

2.3.1 Уравнение Адамса Вильямсона

Допустим, что изменение давления вызвано исключительно весом лежащего выше слоя толщиной , тогда , или . Переходя от конечных приращений к бесконечно малым, получим искомое уравнение Адамса-Вильямсона

(2.7)

Чтобы определить плотность внутри планеты, необходимо

определить продольную и поперечную скорости распространения упругих волн,

вычислить сейсмический параметр,

задать предварительную модель Земли и вычислить силу тяжести,

численно решить дифференциальное уравнение, следовательно, уточнить модель Земли.

В заключение приведем основные формулы для построения сейсмологической модели Земли.

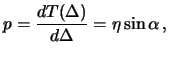
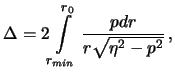
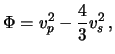
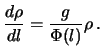
Модель Земли, в общих чертах, выглядит так, как это показано на рис.4. Видна тень сейсмических волн от внешнего, жидкого ядра, простирающая от 103 до 142 градуса эпицентральных расстояний. Именно эта тень была первым доказательством существования жидкого яра Земли.